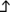heinz hat geschrieben: 
07.01.2019 23:18:54
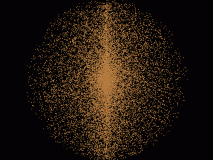
Lassen wir mal die haeufung der Punkte in der Mitte ausser acht.
Wie muesste denn die Formel aussehen um fuer x, y und z verschiedene Radien angeben zu koennen, ohne das ein Kreuz entsteht?
Du musst präzise formulieren, was du haben willst. Dann hast du auch schon die Lösung gefunden.
Du schreibst
gleichverteilt aber sagst nicht genau, was du darunter verstehst.
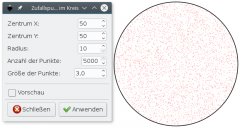
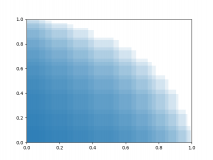
Wenn du "auf gleiche Fläche gleich viele Punkte" meinst, ist die Häufung der Punkte in der Mitte schon ein Problem.
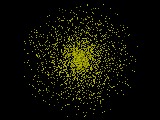
Was du gebaut hast, sieht am Anfang wie "auf gleiche Winkelabschnitte gleich viele Punkte" aus. Aber das machst du dann wieder kaputt, indem du den Punkt nicht dahin setzt, wo er den vorher ausgesuchten Winkel hätte.
Zum Winkel w gehört die Strecke von (0,0) nach (200*cos(w) , 200*sin(w)). Zwischen der x-Achse und dieser Strecke ist der Winkel w. Auf diese Strecke musst du den Punkt setzen, also eine Zufallszahl z zwischen 0 und 1, und dann x=z*200*cos(w) und y=z*200*sin(w).
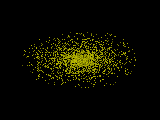
Du hast aber zwei Zufallszahlen z0 und z1 gebaut, und dann x=z0*200*cos(w) und y=z1*200*cos(w) genommen. Das wird dann ein Punkt im Rechteck, wo die Diagonale die Strecke von eben ist. Bei einem Winkel zwischen 0 und 5 landet der Punkt irgendwo nahe der rechten x-Achse. Und bei einem Winkel zwischen 85 und 90 landet der Punkt irgendwo nahe der oberen y-Achse. Bei einem Winkel zwischen 40 und 50 landet er irgendwo im Rechteck, das fast ein Quadrat ist, also genauso häufig an einer Achse wie am anderen Ende des Rechtecks oder in der Mitte davon. Deshalb bekommst du das Kreuz.
Das Einfachste ist mMn Montecarlo. Du nimmst solange zwei Zufallszahlen z0 und z1 zwischen 0 und 1, bis z0^2+z1^2 < 1, dann rechnest du x=200*z0 und y=200*z1. Beim Kreis schmeißt du nur ein gutes Fünftel der Paare von Zufallszahlen weg.
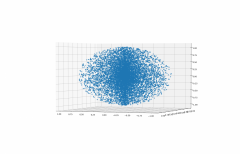
Ellipsoid geht genauso. Da wiederholst du, bis du (z0/a)^2+(z1/b)^2+(z2/c)^2 < 1 hast.
Montecarlo macht man da, wo man früher integrieren musste. Das funktioniert nicht nur da, wo man das Integral nicht anders lösen kann. Das ist die Kanone, mit der man jeden Spatz trifft. Ein paar Millionen mal drauf geschossen und ausgezählt, ist heute eine Frage von Sekunden.